To prove that time period of a simple pendulum is independent of (i) mass of the pendulum (ii) amplitude of the vibration.

 

Abstract

This experiment aims to demonstrate that the time period of a simple pendulum remains constant and is independent of both the mass of the pendulum and the amplitude of its vibration. By conducting controlled experiments, the fundamental principles of pendulum motion can be verified.

Introduction

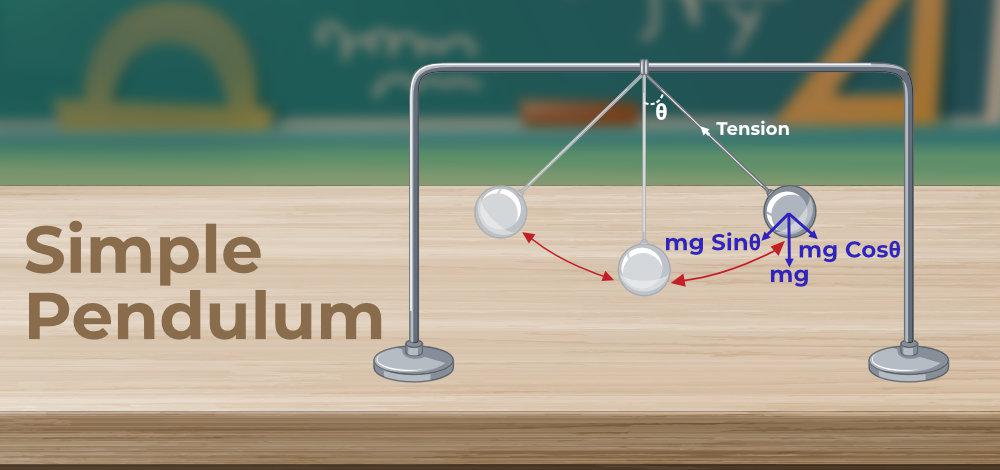
A simple pendulum consists of a mass (bob) attached to a string or rod suspended from a fixed point. The time period of a simple pendulum is the time taken for one complete oscillation. This experiment investigates whether the time period remains constant under variations in mass and amplitude.

Procedure

1. Set up a simple pendulum by suspending a bob from a fixed support.
2. Measure the length (\( L \)) of the pendulum from the point of suspension to the center of the bob.
3. Displace the pendulum to small angles (e.g., 10°) and release it.
4. Measure the time (\( T \)) taken for a certain number of oscillations (\( n \)).
5. Repeat the experiment for different masses of the pendulum while keeping the length and amplitude constant.
6. Repeat the experiment for different amplitudes of vibration while keeping the length and mass constant.

Observations and Conclusions

Observations should show that regardless of changes in mass or amplitude, the time period of the pendulum remains constant, confirming that it is independent of both factors. This supports the fundamental principle of simple harmonic motion.

Short Questions with Answers

1. What is the time period of a simple pendulum?
   Answer: The time taken for one complete oscillation.
2. What factors affect the time period of a simple pendulum?
   Answer: Length of the pendulum and gravitational acceleration.
3. What is the formula for calculating the time period of a simple pendulum?
   Answer: \( T = 2\pi \sqrt{\frac{L}{g}} \).
4. Why is the amplitude of vibration kept small in this experiment?
   Answer: To ensure the motion remains simple harmonic and the pendulum follows the sine law.
5. What does it mean for the time period of a pendulum to be independent of mass?
   Answer: It means the mass of the pendulum does not affect its time period of oscillation.
6. What does it mean for the time period of a pendulum to be independent of amplitude?
   Answer: It means the amplitude of the pendulum's oscillation does not affect its time period.
7. How does the length of the pendulum affect its time period?
   Answer: Longer pendulums have longer time periods.
8. What is the SI unit of time period?
   Answer: Second (s).
9. What precautions should be taken during the experiment?
   Answer: Ensure accurate measurements, minimize air resistance, and use a stable support for the pendulum.
10. Why is it important to measure the time for multiple oscillations?
    Answer: To reduce timing errors and obtain a more accurate average time.
11. What is the purpose of varying the length of the pendulum in the experiment?
    Answer: To demonstrate the independence of time period from pendulum length.
12. What does the independence of time period from mass imply about pendulum motion?
    Answer: It implies that mass does not influence the regularity of pendulum motion.
13. How does the amplitude of vibration affect the motion of the pendulum?
    Answer: It affects the swing of the pendulum but not its time period.
14. What is the significance of keeping the angle of displacement small?
    Answer: To ensure the motion of the pendulum remains simple harmonic.
15. How does the acceleration due to gravity affect the time period of a pendulum?
    Answer: It influences the time period indirectly through the pendulum length.
16. What role does the length of the pendulum play in its time period?
    Answer: Longer pendulums have longer time periods due to increased swing distance.
17. What does the formula for the time period of a pendulum indicate about its dependence on length?
    Answer: It shows that the time period is directly proportional to the square root of the pendulum length.
18. How does changing the mass of the pendulum affect its time period?
    Answer: It does not affect the time period, as demonstrated in the experiment.
19. What factors might introduce errors in the experiment?
    Answer: Air resistance, friction at the pivot, and variations in gravitational acceleration.
20. What is the expected relationship between length and time period?
    Answer: Direct proportionality; longer pendulums have longer time periods.

Multiple Choice Questions with Answers

1. What is the primary factor that affects the time period of a simple pendulum in this experiment?
   1. Mass of the pendulum
   2. Length of the pendulum
   3. Amplitude of vibration
   4. Material of the pendulum
   Answer: B. Length of the pendulum
2. Why is the amplitude of vibration kept small in the experiment?
   1. To increase the time period
   2. To ensure simple harmonic motion
   3. To decrease the time period
   4. To vary the time period
   Answer: B. To ensure simple harmonic motion
3. What does it mean for the time period of a pendulum to be independent of mass?
   1. It decreases with increasing mass
   2. It increases with increasing mass
   3. It remains constant regardless of mass
   4. It varies randomly with mass
   Answer: C. It remains constant regardless of mass
4. How does the length of the pendulum affect its time period?
   1. Longer pendulums have shorter time periods
   2. Longer pendulums have longer time periods
   3. Pendulum length has no effect on the time period
   4. The time period is inversely proportional to the pendulum length
   Answer: B. Longer pendulums have longer time periods
5. What is the significance of measuring the time for multiple oscillations?
   1. To increase the accuracy of the measurement
   2. To decrease the time period
   3. To vary the amplitude of vibration
   4. To increase the mass of the pendulum
   Answer: A. To increase the accuracy of the measurement